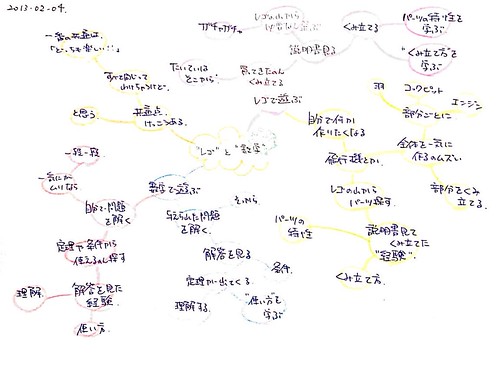
レゴと数学

ぼくはレゴが好きだ。

もうすっかり大人になった今でも、あのブロックたちを見ると心が躍り、何かを組み立てたくなる。

レゴで遊ぶ

今でこそレゴブロックの山を見たら心躍るが、はじめは違ったに違いない。

レゴを見ても、どう使えば良いのか、どう遊べば良いのかわからない。何がどうなってどうなっていくのかわからない。

たいていは買ってきたレゴブロックを、中に入っている説明書通りに組み立てる。説明書にそって、レゴの山から必要なブロックを選ぶ。そして組み立てる。

手順を間違えない限り、車なら車が、お城ならお城が出来上がる。

その過程で、いろんなことを学んでいく。

パーツの特性なり、典型的な”組み立て方”なり。

■自分で何かつくりたくなる

そうして遊び、学んでいくうちに、説明書にそって創るだけではもの足りず、自分で何かをつくりたくなる。飛行機ないし、ロボットないし。

自分のイメージした物に近づけるために、レゴの山からパーツを探していく。使えるのは、山の中にあるパーツのみ。それらを総動員して組み立て、ときには壊しながらつくっていく。

全体を一気に組み立てのが難しければ、飛行機の羽やコックピット、エンジンを別々につくっていく。部分ごとに。部分どうしを組み立てると、全体ができてくるように。

組み立て方はなんだっていい。

そこで必要になるのは、説明書をみながら組み立てたときの”経験”ということになる。

パーツの特性ないし、”組み立て方”ないし。



数学もレゴと似ている、部分がある。

数学で遊ぶ

今でこそ数学を見たら心躍るが、はじめは違ったに違いない。

数学の定理を見ても、どう使えば良いのか、数学の問題を見ても、どう考えていけば良いのかわからない。何がどうなってどうなっていくのかわからない。

たいていは提示された問題を、その問題の解説を聞き、必死に理解する。解説にそって、定理から必要なものを選ぶ。そして論理の組み立てをなぞる。

理解することができさえすれば、問題の結論に至る。

その過程で、いろんなことを学んでいく。

定理の特性・使い方なり、条件の見方・典型的な論理の”組み立て方”、流れなり。

■自力で解きたくなる

そうして遊び、学んでいくうちに、解説にそって理解するだけではもの足りず、自力で解きたくなる。関数の問題ないし、幾何の問題ないし。

自力で問題を解き進めるために、条件を眺め、使える定理をさぐる。使えるのは、問題文中にある条件と、定理のみ。それらを総動員して組み立て、ときには壊しながらつくっていく。

全体を一気に組み立てるのが難しければ、別々につくっていく。部分ごとに。部分どうしを組み立てると、全体ができてくるように。

組み立て方はなんだっていい。

そこで必要になるのは、解説をみながら理解したときの”経験”ということになる。

定理の特性・使い方ないし、条件の見方・論理の”組み立て方”ないし。



もちろんレゴと数学は大きく違う。

レゴは嫌われていないし、難しくない。

おわりに

共通点はけっこうあると思う。もしかしたら、だからぼくは両方好きなのかもしれない。

結論めいたものはなにもないけど、このへんで。

では、お読みいただきありがとうございました。

RSS