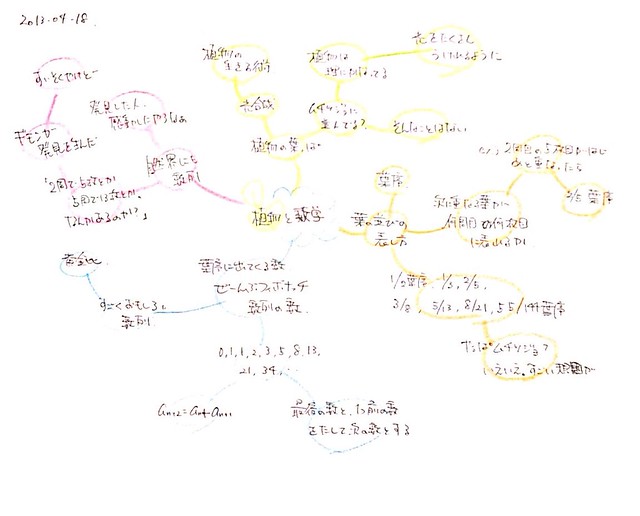
植物と数学

太陽の光を浴びて、スッと伸びて立っている草花は、見ていて美しさを感じる。

その「きれいやなぁ」という感覚は、鮮やかな色彩による部分が大きく、それに加え、規則的に中心から広がった花びらたちや、茎から伸びる葉の様子が、色とあいまって綺麗に映る。

無秩序ではなく、規則的に、理にかなった姿形が。

葉の並びの表し方

葉は、すべてがそうというわけではないが、上からみると四方八方に広がっている。



ただただ無秩序に葉を広げているわけではなく、そこにはちゃんとした順序がある。これも種類によって様々なものがあるが。

その順序を表したのが「葉序」。

”次に重なるのが、何周目の何枚目に現れるか”によって、その葉序は表される。

例えば、上から見た時に、2周目の5枚目がはじめの葉と重なるようであれば、「2/5 葉序」というように。



草の種類によって、いろんな葉序のものが存在する。

1/2葉序や、1/3葉序、2/5葉序に3/8葉序、5/13葉序もあり、8/21葉序も、大きい数については55/144葉序まで。

なんだかいっぱい数字が出てきて、やっぱり規則なんてなさそうに、そこには秩序なんてないように見える。でも、実はちゃんと規則が備わっている。

フィボナッチ数列

話は変わるが、”フィボナッチ数列”をご存知だろうか？

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,....

これがフィボナッチ数列。この数の並びには、しっかりと規則がある。

最後の数と1つ前の数を足して、次の数とする

数列が、フィボナッチ数列。

3項目と4項目を足して5項目になり、4項目と5項目を足して6項目になり。。。そんな数列。

フィボナッチ数列は、黄金比とも関係してくるとても興味深い数列で、実は今回の「葉序」にもそのフィボナッチ数列が見受けられる。

植物の世界と数学の世界が、この「フィボナッチ数列」によって結び付けられる。

葉序とフィボナッチ数列

もう一度葉序に戻ると、草の種類によって、1/2葉序や、1/3葉序、2/5葉序に3/8葉序、5/13葉序もあり、8/21葉序も、大きい数については55/144葉序まで存在する、と述べた。

ここに出てきている数をよぉく見てみて欲しい。

1, 2, 3, 5, 8, 13もあるし、21も。55や144まで。

そう、葉序に出てくる数はどれも、フィボナッチ数列に出てくる数の中に存在する。

すごい。

これを初めて知ったとき、「関係があるなんて考えたことがなかった植物と数学にはこんな関係があるなんて！」と感動してしまった。

そんな感動を少しでも感じてくれたらすんごくうれしい。

おわりに

自然界にも数学がある。

初めて知って感動した次に思ったことが、「初めてこれを発見した人の感動と言ったら、ものすごいやろうなぁ」ということ。

ぼくの感動の比ではないくらいに驚き、興奮し、感動したにちがいない。

その感動を、ちょっとでも垣間見れたことが嬉しい。

そんな嬉しさを、数学を教えることを通して多くの人に伝えることができたらなぁと思う。

では、お読みいただきありがとうございました。

RSS