MF03:視点を変えると捉え方が変わる。それもまたおもしろ

はいきました3回目の連載。今日も数学のおもしろいところについて書いていくことにします。お付き合いくだされば幸いです。それでは、レッツゴー！

なんの変哲もない式でも、、、

みなさん、この式を見たことがあるでしょうか？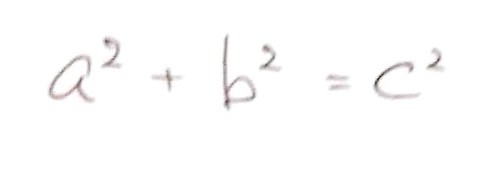




はい、これは「ピタゴラスの定理」というものです。式として眺めるだけなら、これ以上でもこれ以下でもありません。あくまで式として眺めるだけなら。

でも、皆さんご存知のように、ピタゴラスの定理は、次のような”図形”に対して成り立つ式なんですよね。




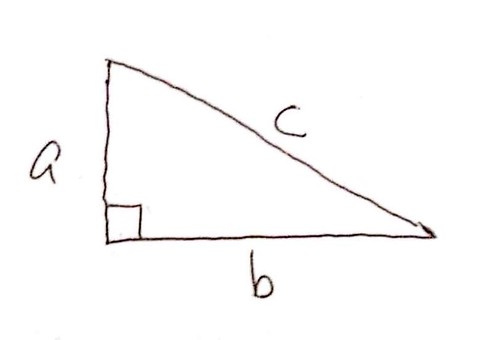
式をただ単に”式そのもの”として捉えるだけだと、無機質でなんの面白みもありません。でも、別の視点で、例えば”図形”の世界から式を捉えてみると、特徴的なことが明らかになったりする。これも数学をしていておもしろいなぁと感じる点です。

で、この「ピタゴラスの定理」は、直角三角形において成り立つ式として認識されていますが、すこーしだけ見方を変えれば「長方形の各辺とその対角線に置いて成り立つ式」と捉えることもできます。

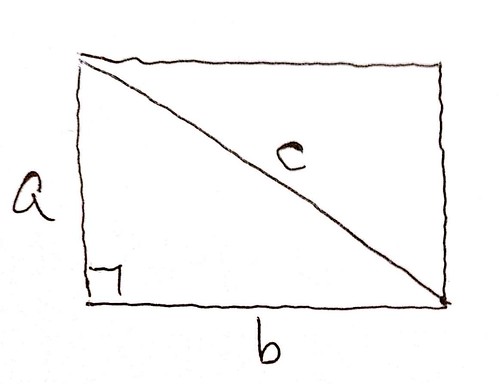
では、次のなんの変哲もない式を。

ではちょこっと思考を進めていきます。先ほどの式では、左辺は"a"と”b”の2つの値について成り立つものでしたが、ここでこんな疑問を考えてみたりします。

「2つで成り立ったときおもしろいことがわかったんなら、じゃあ次3つだったらどうなるだろう？」と。




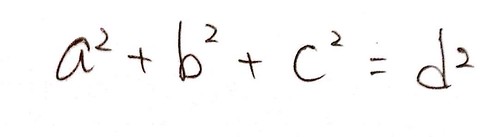
こういう疑問が湧けば、実際に考えるのみです。この式も、ただ単に”式として”とらえるよりも、やっぱりさっきの経験から、図形とからめて考えてみるのが良さそうです。だって左辺の値が一つ増えただけで、ピタゴラスの定理となんだか似てますものね。

図形の世界で先ほどの式を捉えてみると、実はこんなことがわかってきます。




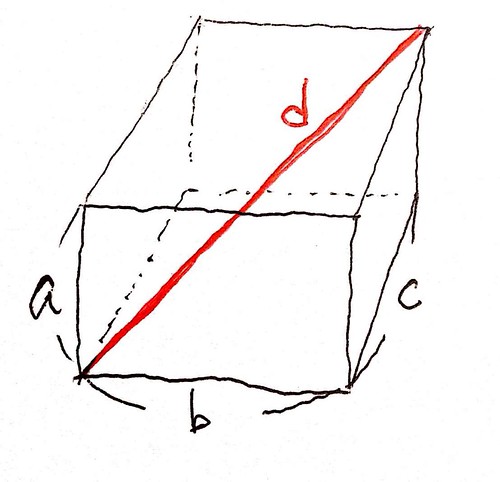
「直方体の各辺と、その空間の対角線に置いて成り立つ式」を表すものだったんです。ん？似てますね。




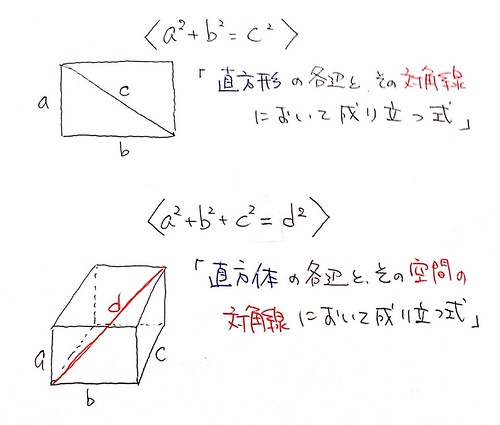
式自体を見て、それを同じ”図形”の世界から捉えてみると、その結論も似たようなことがわかったりする。そういうのんが「驚き」や「発見」を与えてくれる。驚いたり発見したりすると、「うおー！すげーっ！！」ってなったりしませんか？そんな感覚を数学は確かに与えてくれます。

だからなに？

見方を変えると、数学の世界は拡がっていき、つながりが見えてきて、いろんな発見に出会えます。

はじめから自分で、いろんな見方で、視点で式を捉えていくのはたしかに難しい側面があります。でも、学ぶ中で見方を変えると拡がる世界ってのを感じて欲しい。そんな思いで、これからも楽しさを伝えていくのみですね。

では、お読みいただきありがとうございました。

RSS